You write code, you know what you're doing... That just makes you a smart writer.
Not so different from a no-coder or a vibe-coder.

If you really want to up your game – or ace that FAANG interview – you really need to understand how efficient your code is.

The programming language is irrelevant.

What actually matters is the data you're handling, and how efficiently you handle it.

Allow me to illustrate:

Have you played that game, where you need to guess a number between 1 and 100
What's more efficient?

- counting from one to 100?
- or going 50, 75, 87, 93?

Even if you count very very fast, you'd still be slower than the guy halving the remaining numbers.

But how do you go from the former to the later?

That's the difference between a programmer and software engineer.

Are you ready to take the leap?

Key takeways

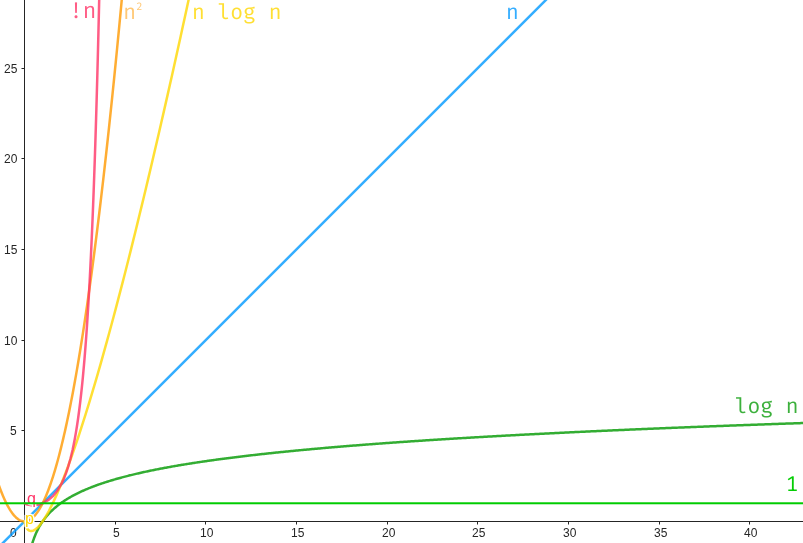
• We evaluate how efficient an algorithm is by "counting" how much time and space the algorithm consumes based on the input \(n\)
• We use Big O to denote the worst case scenario

The method

We could compare:

for (int i = 0; i <= n; i++) {
  if (test(i))
    return i;
}

with

int findInRange(int min, int max) {
  int val = (max - min) / 2;
  int found = test(val);
  
  if (found == 0) return val;
  if (found < 0) return findInRange(0, val - 1);
  return findInRange(val + 1, max)
}

And assume the 1st is "better"

We could also plot the number of operations made per entry:

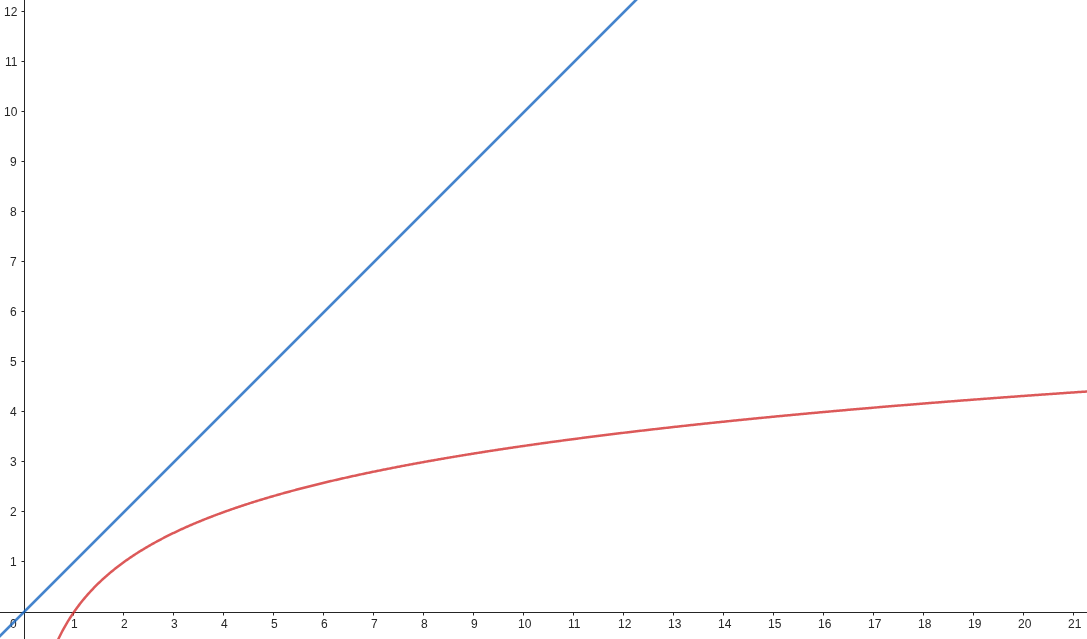
The gap is obvious, and that's just for guessing from 0 to 21.

If we want to measure of efficient an algorithm, we just need to compare how many operation each would make for \(n\) entry.

That's pretty much it.

The 1st (blue) does \(n\) operation, the second (red) does \(\log_2{n}\) operations.

Instead of plotting each time, we'll say blue runs in \(O(n)\) and red in \(O(\log_2{n})\).
Actually we'll say Big O of \(n\) and Big O of \(\log{n}\).

Well, if we wanted to be pedantic, we'd say \(\Theta(n)\) and \(\Theta(\log{n})\), but that's a story for a tad later 😉

Now, in the intro, I said it's the order of magnitude that matters. Well constants basically don't affect the order of magnitude, so we can ignore them. \(O(2n)\) is basically equivalent to \(O(\frac{n}{2})\).

We note both \(O(n)\)

Let's practice shall we?

What's best to practice than a problem? Namely: The egg drop problem

You have two eggs and a building of \(n\) floors.
How would you determine at which floor the eggs would break?

Note:
- Those are not your standards eggs. You can throw them from the same floor how many time you'd like and if they don't break, they will never break from the same floor.
- You can conveniently teleport to any floor you'd like at no cost at all.

Let's break it down

What if we had one egg...

We'd go from floor to floor and try whether the egg breaks or not.

• Best case scenario, it'd break on the 1st floor, and we'd do 1 throw
• Worst case scenario, it'd break on the last floor, and we'd do \(n\) throws
• On average it'd break at the \(k^{\text{th}}\) floor (where \(k \le n\)), and we'd do \(k\) throw

Because an algorithm is as good as its worst case, this solution runs in \(O(n)\).

What if we had an infinity of eggs?

We covered this one already, it's the same as the guess the number. We have an infinite number of try:

• Best case, the egg breaks on the \(\frac{n}{2}\) floor
• Worst case, the egg breaks on the \(\log_2{n}\) floor
• Average case, the egg breaks on \(\log_2{k}\) floor where \(k \le n\)

So basically this methods runs in \(O(\log_2{n})\)

Let's mix both methods with two eggs

We could split the building in \(k\) sections of \(k\) floors.
We'd go from section to section and when egg #1 breaks, we'd go from floor to floor, starting but only from that sections.

If we had 100 floors, we'd do 10, 20, 30, 21, 22, 23 done.

• Best case, the egg breaks on floor \(k\) and we'd do 1 throw
• Worst case, the egg breaks on the floor before last and we'd do \(2k\) throw

And because \(n = k_\text{sections} \cdot k_\text{floors} \iff k = \sqrt{n}\). Which means we'd do \(2\sqrt{n}\) throws.

This one runs in \(O(2\sqrt{n})\).

By the way, the order of magnitude is more relevant than the actual efficiency. There's no "real" difference between \(O(2\sqrt{n})\) and \(O(\sqrt{n})\).
At least, not when it comes to comparing the three algorithms we got so far.

Is there better?

Actually not much, with two eggs at least.
However we can improve a tad more the last one.

There's a bit of a discrepancy in the numbers of throw if the eggs breaks in the lower floors, than in the higher floors.

For example, if the egg breaks in the 14th floor of a 100 story building, we'd have throw:

10, 20, 11, 12, 13, 14 \(\Rightarrow\) 6 throws

And if it breaks on the 94th floor, we'd have throw:

10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 91, 92, 93, 94 \(\Rightarrow\) 14 throws

Surely we could reorganize stuff around.

The rational is each next section should have one floor less than the previous, because we'd consume one throw testing the section itself.

In other words: \(n = k + \dots + 3 + 2 + 1\) and we need to solve for \(k\).

$$
\begin{align}
n & = k + \dots + 3 + 2 + 1 \\
n & = \frac{k(k + 1)}{2} \\
0 & = \frac{1}{2}k^2 + \frac{1}{2}k - n \\
x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}
\Rightarrow k & = \frac{-\frac{1}{2}\pm\sqrt{\left(\frac{1}{2}\right)^2-4\cdot\frac{1}{2}\cdot-n}}{2\frac{1}{2}} \\
k & = \frac{-1\pm\sqrt{1+8n}}{2}
\end{align}
$$

Which means this algoritm runs in \(O\left(\frac{-1\pm\sqrt{1+8n}}{2}\right) \approx O(\sqrt{n})\)

Solutions

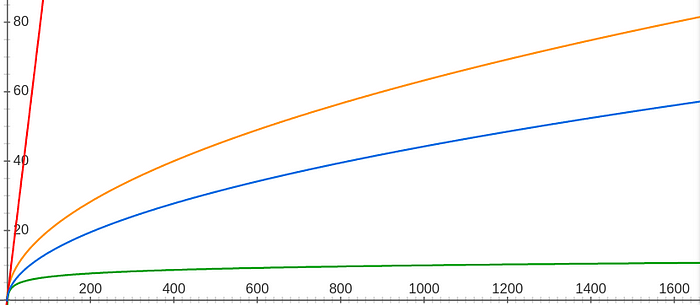
• red: with 1 egg \(\to O(n)\)
• green: with an infinity of eggs \(\to O(\log_2{n})\)
• orange: our first 2 eggs solution \(\to O(2\sqrt{n})\)
• blue: our second 2 eggs solution \(\to O\left(\frac{-1\pm\sqrt{1+8n}}{2}\right)\)

We can clearly see the difference between the \(O(n)\), \(O(\sqrt{n})\), and \(O(\log{n})\) regardless of the constants we dropped. Of course, constants make sense when comparing two algorithms of the same overall complexity (for 1600 floors, there is a 30 try offset between the 1st two eggs solution and the second).

Going further…

Time and space

Up until this point we’ve counted the number of steps. We call this the “time complexity” because it gives a sense of how long the algorithm will take to run.

The same logic can apply to the amount of memory the algorithm would take: “space complexity".

For example

const removeDuplicates = (arr: Array<number>) =>
  arr.sort()                                           // O(n log n)
     .filter((item, index) => index == 0               // arr[0] is unique 
                           || item !== arr[index - 1]) // is prev = current?

This runs in \(O(n\cdot\log{n})\) because of the sort step, but does not require additional memory.

This one however:

const removeDuplicates = (arr: Array<number>) =>
  Array.from(new Set(arr))

Works in \(O(n)\) time (because both Array.from and new Set(Array) work in \(O(n)\) time, but because it uses a Set it also runs in \(O(n)\) space.

If you're wondering, \(O(n\cdot\log{n})\) is worse than \(O(n)\).... like \(\log{n}\) times worse.

The question is: would you sacrifice memory for speed?
I guess it depends of your data.

Big O, little o, Big Theta \(\Theta\), Big Omega \(\Omega\) and Little omega \(\omega\)

I lied to you.

I said we used the Big O notation to evaluate the complexity of an algorithm.

In truth, we use Big O to evaluate the asymptotic tight upper bound of the growth rate of the function...
That basically mean "the closest estimate of the worst case scenario" (ish).

Big Omega is used to evaluate the asymptotic tight lower bound of the growth rate of the function, aka : "the closest estimate of the best case scenario".

little o and little omega are the loose upper/lower bound of the growth function, which basically means, "there cannot be a best/worst case than that"

Big Theta is the tight bound, both upper and lower of function, aka expected average case

In other words, if you have a 2 hours drive:
- \(\omega \rightarrow\) I'll arrive in 1h if I don't respect traffic rules
- \(\Omega \rightarrow\) I'll arrive in 1h30, traffic was surprisingly fluid
- \(\Theta \rightarrow\) I'll arrive in 2h
- \(O \rightarrow\) I'll arrive in 3h, because I'm expecting loads of traffic
- \(o \rightarrow\) I'll arrive in 10h, because it's possible my car will break and I'll have to walk

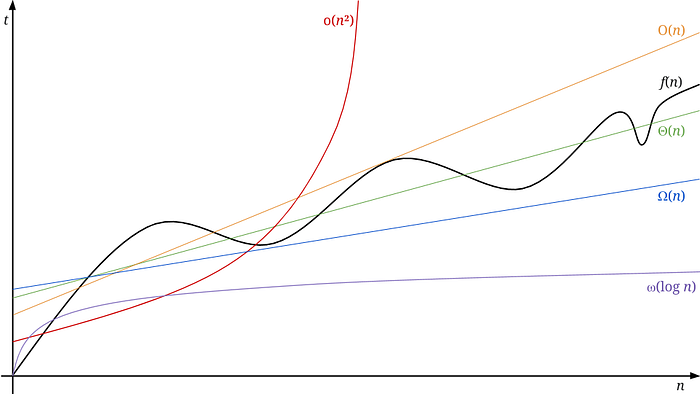
If we look at the graph, our algorithm f(n) runs in Θ(n) and is bounded between O(n) and Ω(n). In the long run, we know it won’t get worse than o(n²) nor better than ω(log n)

Common complexities

• \(O(1)\) direct access (e.g. in an array or a Hashmap / Set)
• \(O(n)\) looping through the input (e.g. index lookup, counting)
• \(O(log{n})\) divide the problem (e.g. binary tree lookup)
• \(O(n\cdot\log{n})\) sorting
• \(O(n^2)\) for each input, look at every other input (e.g. bubble sort)
• \(O(!n)\) combinatorics

Still want more???

https://en.wikipedia.org/wiki/Big_O_notation